A la hora de hacer Tests de Hipótesis Nula, uno de los factores más importantes es seleccionar la hipótesis correcta. En posts anteriores explique que casi todos los valores resultantes de un test de hipótesis nula, como el p-value y los intervalos de confianza, solo pueden ser interpretados en relación a la hipótesis nula seleccionada.

Muchos equipos suelen seleccionar por defecto la hipótesis nula de que la diferencia entre el grupo tratamiento y el grupo control es igual a 0.

Pero esta hipótesis no es la que mejor se alinea al tipo de decisiones que se desea tomar en experimentos en marketing y UX, dado que nos da una interpretación más ambigua o menos exacta respecto a direccionalidad del efecto. A continuación demostraré 3 tipos de hipótesis distintas que en mi opinión son más adecuadas para estos equipos y razonaré los motivos.

Hipótesis de 2 colas (Hipótesis Nula: Diferencia entre grupos es igual a 0)

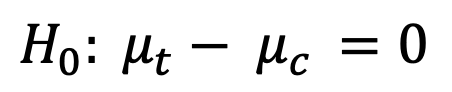
A menudo los motivos por los que experimentamos es porque queremos estar seguros de estar logrando una mejora en alguna métrica relevante, sea CTR, Tasa de Conversión, Tasa de Agregar al carrito, etc. Ejemplos pueden ser cambios en el texto de una página, elementos visuales, experiencias completamente distintas que buscan llegar al cliente desde otro ángulo, contenido personalizado sea generado por data de navegación previa o por modelos de recomendación, entre otras.

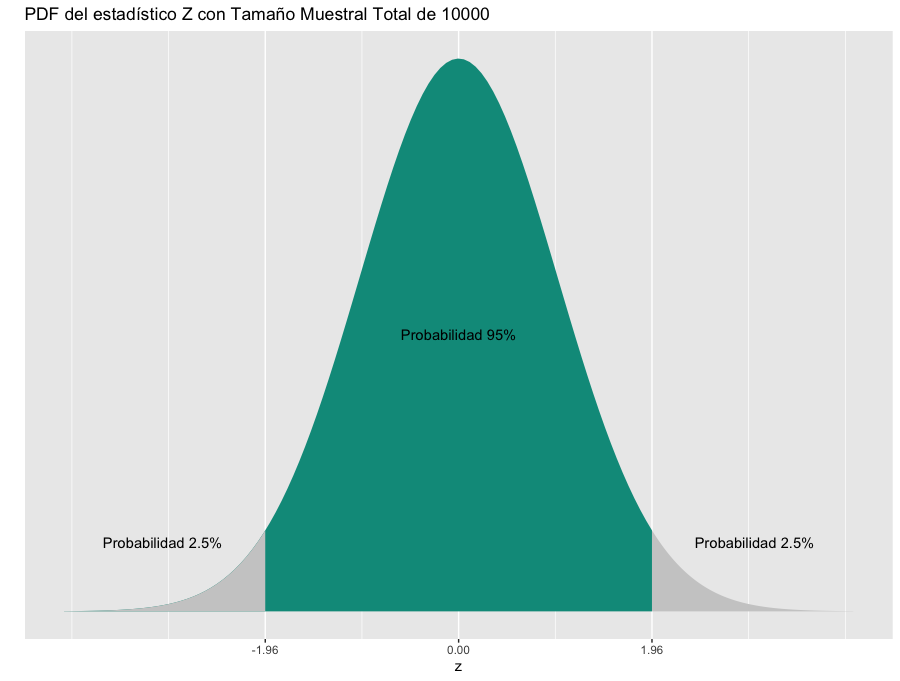
Si utilizaramos la hipótesis nula de que la diferencia absoluta entre los grupos es igual a 0 y un alpha de 5%, nuestro experimento estaría diseñado para ver si observa valores en las siguientes dos zonas de rechazo.

Como pueden ver en el gráfico anterior, estaríamos rechazando la hipótesis nula en dos casos: Si el efecto observado se encuentra en la zona de rechazo por ser muy extremo por lo positivo, o si es muy extremo por lo negativo. Además podrán observar que como nuestro alpha era de 5% pero estamos buscando en dos zonas de rechazo, ese 5% queda dividido en 2, y por lo tanto cada zona de rechazo es de la mitad de tamaño que si fuera una sola del 5%.

Este tipo de test se denomina test de dos colas, justamente porque nuestras zonas de rechazos se ubican en las dos colas de la distribución.

Pero ¿por qué esta hipótesis nula no es la más adecuada para el tipo de experimentos que mencioné antes? Pensemos un segundo cual es el espectro de decisiones posibles que solemos tomar en estas situaciones. Si logramos encontrar un efecto positivo significante, implementamos el cambio. Pero si no encontramos un efecto positivo significante, no lo implementamos y buscamos otras alternativas. Ahora, ¿que pasa si encontramos un efecto negativo significante, que rechaza nuestra hipótesis nula de dos colas, donde asumimos que el efecto es 0? Por ejemplo un valor observado que se encuentra en la zona de rechazo de la izquierda de nuestro gráfico anterior. No implementaríamos el cambio verdad? Por lo tanto, nuestra decisión es la misma tanto si no encontramos un efecto significativo como si encontráramos un efecto significativo negativo. Con eso en mente, no pareciera que un test de dos colas, que disminuye, vuelve más exigente nuestra zona de rechazo positiva, sea la hipótesis más adecuada, ¿cierto?

Veamos entonces qué otras opciones tenemos.

Test de Superioridad (Hipótesis nula de que el efecto es menor o igual a 0)

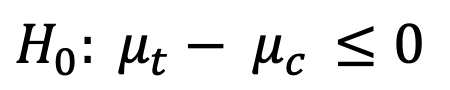
En este tipo de test, se plantea una hipótesis nula en la que asumimos que el efecto entre los dos grupos es 0 o negativo, y por lo tanto vamos a rechazar esa hipótesis si encontramos evidencia significante de que el efecto es mayor a 0. En términos de negocio, estamos asumiendo que por ejemplo, nuestra nueva página de producto, no genera un aumento en la tasa de agregar al carrito o la empeora pero nos gustaría observar que sí hay un efecto y que ese efecto es mayor a 0. Volviendo a tomar un diseño con un alpha de 5% nuestra zona de rechazo se vería de la siguiente forma:

En este gráfico podemos observar que nuestra zona de rechazo es del 5% solo hacia el lado derecho (por eso este tipo de test pertenece a los denominados “de una cola”). Ahora, al estar todo el alpha concentrado en un solo lado, al exigencia para rechazar la hipótesis nula por superioridad es menor a la de un test de dos colas con mismo alpha. Esto lleva a creer erróneamente que los test de una cola están “sesgados” a encontrar valores hacia una determinada dirección. Esto de ninguna forma es cierto, dado que el alpha seleccionado es quien determina la zona de rechazo, y el mismo debe ser elegido a priori bajo el contexto del problema que se quiere resolver, sea 5% , 2,5% o 50% , pero no afecta a cuál será el valor efectivamente observado.

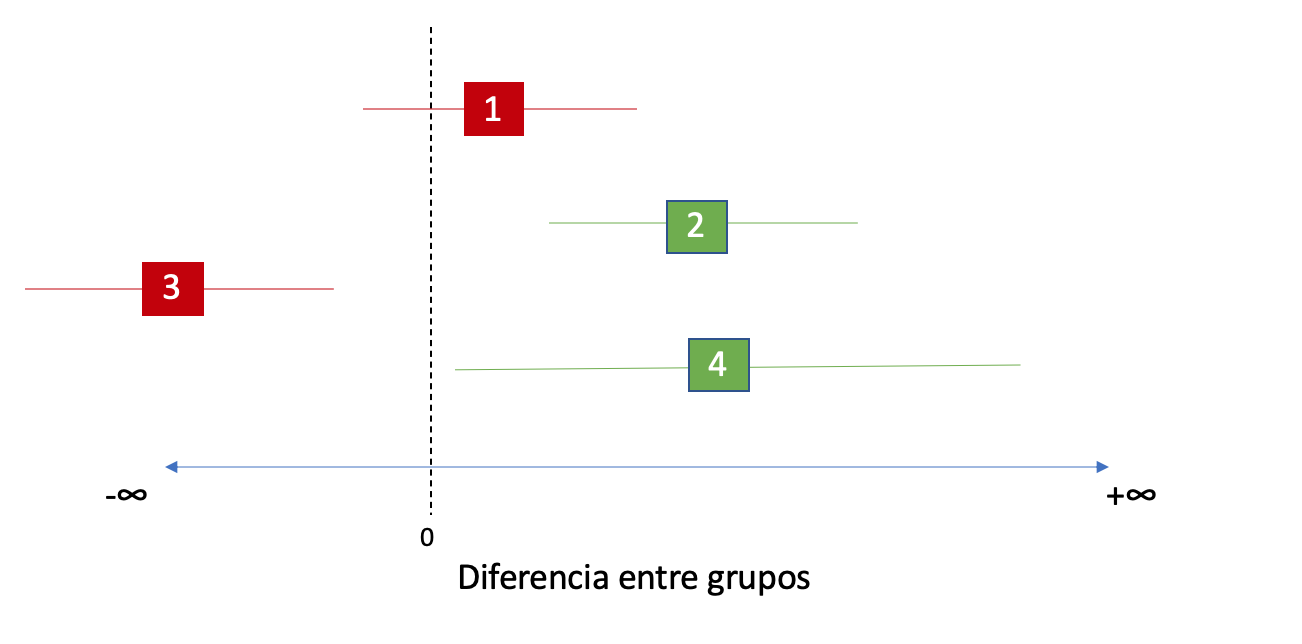
Por otro lado, los test de una sola cola, como en este caso, un test de Superioridad, también tienen su interpretación respecto a los intervalos de confianza. Dado que no solo nos interesa rechazar la hipótesis nula, sino también tener una estimación de la magnitud del efecto, podemos calcular los intervalos de confianza “de una sola cola”. En los test de superioridad, estos intervalos nos brindan un valor limitante por lo bajo, y en general suelen limitarse por lo alto en +∞. ¿Qué significa esto? Que valores menores al límite inferior del intervalo no son soportados por los datos del experimento. Por lo tanto, si rechazamos la hipótesis nula de que el efecto es menor o igual a cero con alpha de 5%, el intervalo de confianza al 95% será tal que su límite inferior debe ser mayor que cero. En la siguiente imágen encontrarán algunos ejemplos.

Cada línea numerada es un intervalo de confianza al 95% distinto. Las líneas 1 y 3 son de experimentos que no rechazaron la hipótesis nula de ejemplo (p-values mayores a 0,05). En estos casos vemos como la línea 1, si bien su promedio observado (la cajita) se encuentra por encima del 0, el límite inferior de su intervalo de confianza es menor a 0, y por lo tanto no logra excluir al 0 de su rango. En el caso de la línea 3, representa un grupo donde el efecto observado y el intervalo de confianza fueron ampliamente inferiores a 0. A su vez, los intervalos 2 y 4 representan experimentos que sí lograron rechazar la hipótesis nula de que el efecto es menor o igual a 0. La línea 2 representa un caso donde la hipótesis se rechazó ampliamente, dada su distancia al 0, mientras que la línea 4 representa una superioridad más débil. Y su línea es más larga y por ende menos precisa debido a una mayor varianza o a un menor tamaño muestral.

Con estos ejemplos podemos ver entonces que un intervalo de confianza de una sola cola nos permite tener un mejor entendimiento del efecto mínimo soportado por los datos, y cuán distante ese límite inferior está del 0. Esta distancia nos da lugar a explicar un segundo tipo de hipótesis de una sola cola.

Test de Superioridad Fuerte

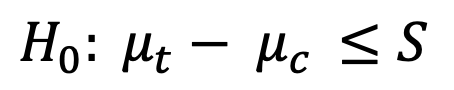
En el caso anterior estábamos asumiendo una hipótesis nula donde el efecto del tratamiento es menor o igual a 0, con el fín de detectar que el tratamiento tiene un efecto positivo, sea cual sea el tamaño de este efecto.

Ahora bien, existen casos, donde no nos alcanzará con detectar solo la presencia de una direccionalidad de efecto positivo, sino que lo que buscaremos lograr, es probar que hay un efecto considerablemente mayor. Cuan considerable dependerá del caso. Podría ser un efecto mayor a 2, a 5, a 20, lo que sea que haga sentido para el negocio. Este valor lo llamaremos margen de superioridad y lo indicaremos con la letra “S”.

Por ejemplo, supongamos que nuestro equipo de data scientist desarrolló un modelo de recomendación de productos que se cree mejor que el que existe en la página de producto actualmente. El equipo tiene muchos fundamentos para creer que su modelo debería performar mejor que el actual, pero tiene el inconveniente de que para poder tenerlo en producción para todos los usuarios, hay que invertir tiempo y recursos en infraestructura para el procesamiento de datos y para su uso en el sitio web. Si siguiéramos en el caso anterior, y solo nos preocupa que haya un efecto positivo, nuestra hipótesis nula seguiría siendo que el efecto es igual o menor a cero.

Pero en este caso, con todos los costos necesarios, queremos garantizar que si aplicamos el modelo de nuestros data scientists, el efecto generado sea lo suficientemente grande para justificar sus costos adicionales. Es por eso que vamos a proponer una hipótesis nula según la cual el efecto (diferencia entre los grupos) es menor o igual a 2% (por ejemplo que la tasa de conversión pase de ser 1% a por lo menos 3%).

¿Que efectos tiene esto en nuestro experimento? A nivel del diseño experimental, hay que tener en cuenta que hacer un test de superioridad fuerte va a requerir un tamaño muestral mayor que un test de superioridad simple. Esto es porque en efecto estamos achicando el Efecto Mínimo Detectable real, y si recuerdan las fórmulas que mencioné en posteos anteriores, cuanto más chico es el Efecto Mínimo Detectable, más grande debe ser el tamaño muestral según el cálculo de potencia. Por lo tanto, cuanto más grande sea la superioridad que seleccionemos, más observaciones requerirá nuestro experimento. Asique elegir el tamaño de la superioridad debe hacerse con criterio que haga sentido al negocio y su contexto.

Respecto a cómo se evalúa un test de superioridad fuerte, el cálculo es muy simple. Al calcular el estadístico de prueba (valor Z, valor T, etc) solamente debemos restarle al efecto observado la superioridad que decidimos en el diseño. Ejemplo:

Grupo	Visitas	Tasa de Conversión
Control	10000	5%
Variante	10000	5.55%

Si hiciéramos un test de superioridad simple, el efecto observado sería 0,0555 - 0,05 y el p-value resultante sería: 0,04. Pero cómo decidimos hacer un test de superioridad fuerte, mayor a 0.7 puntos porcentuales, nuestro efecto observado ahora se calcula 0,0555 - 0,05 - 0,007, y el p-value de este efecto es 0,68, que no es significante a un alpha de 0,05. Como podrán imaginar , los test de superioridad fuerte son más exigentes respecto a los rechazos de la hipótesis nula y requieren un mayor tamaño muestral, pero dan cuenta no solo de la dirección del efecto, sino de un límite inferior del intervalo de confianza más distante del 0 (línea 2 en nuestra imágen previa).

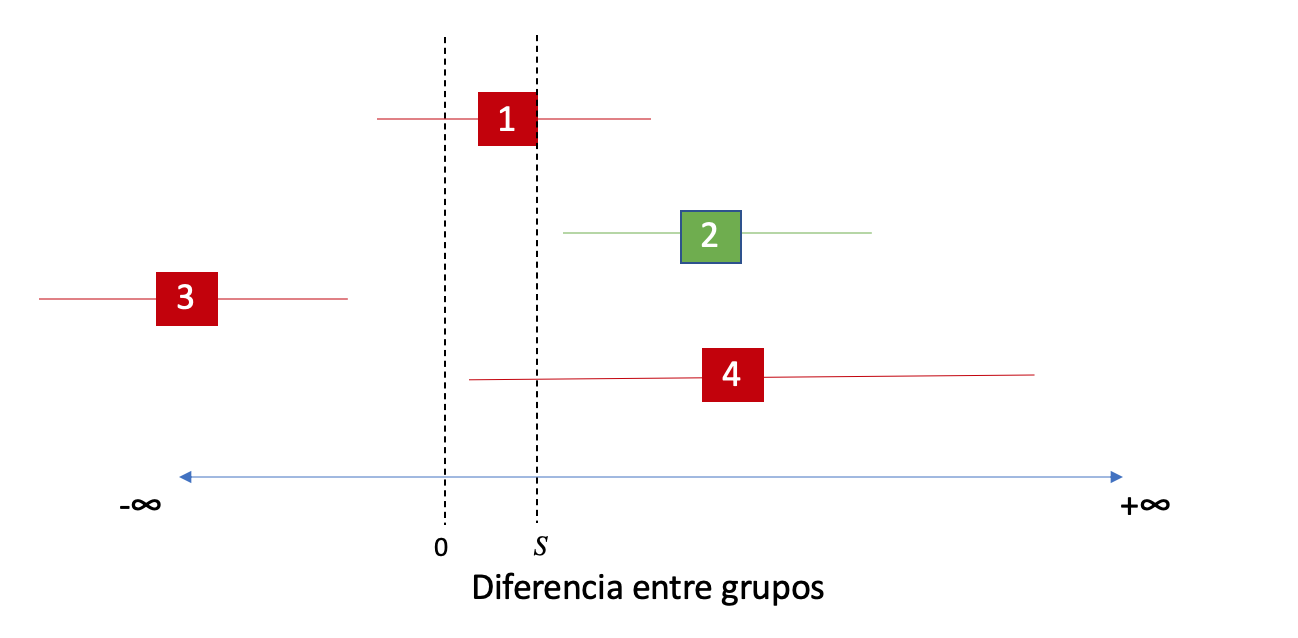
Respecto a los intervalos de confianza, el Test de Superioridad Fuerte “mueve” el límite inferior mínimo necesario para rechazar a la hipótesis nula hacia la derecha, por lo tanto en el caso de nuestros intervalos de la imágen anterior, ahora los resultados serían:

Ahora el único intervalo que rechaza la hipótesis nula es el número 2, ya que es el único a la derecha de nuestro margen de superioridad S.

Otros ejemplos de cuándo es adecuado hacer un test de superioridad fuerte son:

1. Una vez aplicado el cambio es difícil de revertir
2. Quien está a cargo de tomar la decisión es escéptico del valor posible que pueda generar ese cambio
3. Hay mucha resistencia respecto a implementar dicho cambio por parte de varios stakeholders.

Test de No Inferioridad

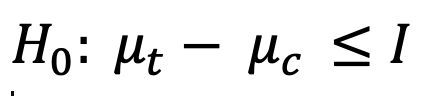
Por último, tenemos otro caso de negocios que muchas veces suceden y sin embargo no son evaluados. Supongamos que algunas secciones de nuestro sitio web, ecommerce, blog, etc, están programadas en código desactualizado, que si bién funciona, podría ocasionar riesgos de seguridad. O por ejemplo, que hay ciertos elementos visuales que por cuestiones de definición de marca deben ser reemplazados. En ambos casos, no nos interesa mejorar ninguna métrica en particular, pero si nos interesa que al realizar el cambio, esa determinada métrica no disminuya por debajo de un valor específico. En estos casos, es donde podemos hacer uso de Tests de No Inferioridad.

Este tipo de tests es muy similar al test de superioridad fuerte, solo que como se podrán imaginar, el margen que nos interesa fijar no va a ser un margen de efecto positivo, sino un margen de efecto negativo, al que llamaremos margen de no inferioridad, que representa cuánta es la diferencia negativa máxima del efecto que estoy dispuesto a soportar.

Tal como en el caso de Superioridad Fuerte, su cálculo es bastante simple. Al calcular el estadístico de prueba (valor Z, valor T, etc) esta vez debemos sumarle al efecto observado nuestro margen de inferioridad decidido. Ejemplo:

Grupo	Visitas	Tasa de Conversión
Control	10000	5%
Variante	10000	5.3%

Si hiciéramos un test de superioridad simple, el p_vaue sería de 0,17. Pero al tomarlo como un test de No Inferioridad con un margen de - 0.25 p.p, nuestro efecto observado ahora se calcula 0.053 - 0.05 + 0.0025, y el p-value de este efecto es 0.04. Al ser un caso contrario al de superioridad fuerte , los test de no inferioridad son menos exigentes respecto a los rechazos de la hipótesis nula y requieren un menor tamaño muestral. A cambio, en caso de rechazar la hipótesis nula estamos asumiendo un riesgo de tamaño alpha de estar implementando un cambio que quizás no tiene un efecto real o tiene un efecto real negativo entre el margen seleccionado y 0.

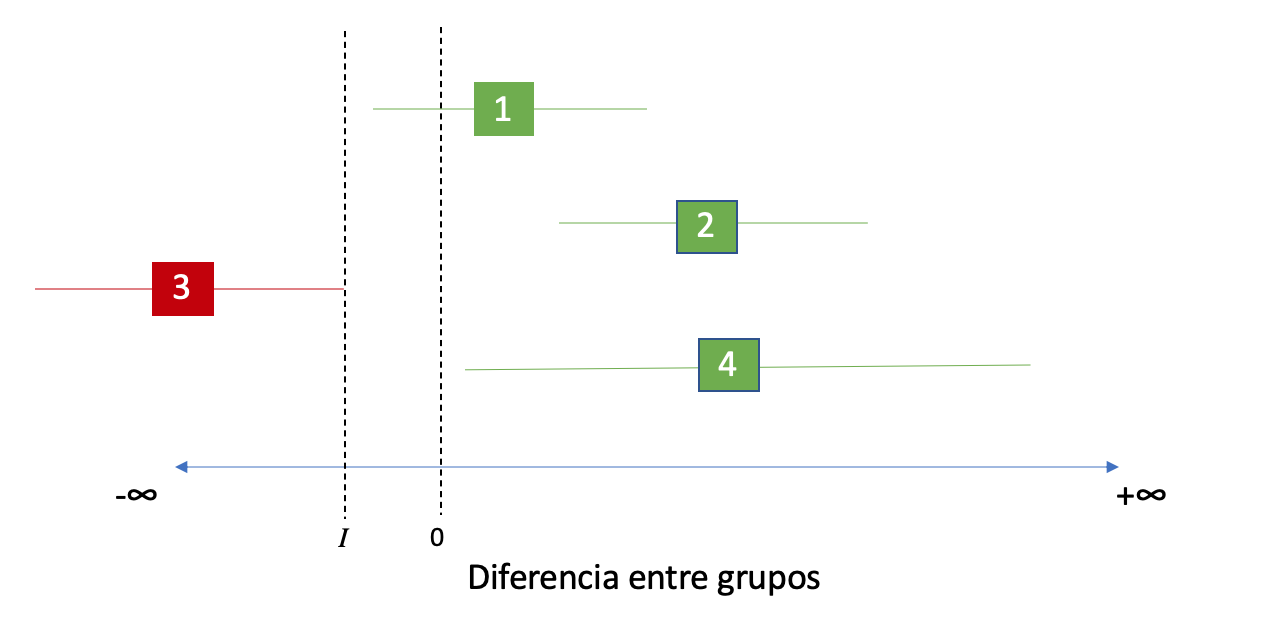
Volviendo a la imágen de los intervalos de confianza, en este caso tanto el 1, el 2 y el 3 rechazan la hipótesis nula, dado que su límite inferior se encuentra a la derecha de nuestro margen de Inferioridad I.

Seleccionar nuestra hipótesis

Habiendo explicado los distintos tipos de hipótesis que se pueden seleccionar a la hora de diseñar un Test de Hipótesis Nula, espero que se sientan más preparados para abordar distintos casos de experimentación dentro de sus equipos. Lo más importante es que se tomen el tiempo para poder identificar cual es la hipótesis correcta en su caso específico, reconozcan los beneficios y efectos que tiene seleccionar una determinada hipótesis sobre otra, y tener confianza de que el diseño experimental que decidieron es el que mejor aborda la incertidumbre que intentan resolver y por lo tanto el que más ayuda a darle luz a la toma de decisiones que tienen por delante.

---

Gracias por leer mi blog!

Si te gustó lo que leiste te invito a que te sumes al newsletter para recibir un mail semanal con el nuevo contenido y novedades. O podes apoyarme con su desarrollo invitandome un cafe :) Muchas gracias!

Subscribirse