Este articulo esta basado principalmente en los escritos y presentaciones de Matt Gershoff, fundador de Conductrics https://conductrics.com quien me autorizó a utilizar sus ideas y material. Pueden encontrar su presentación sobre este tema en el siguiente link. Los invito a que visiten su blog en el sitio de Conductrics, ya que contiene material didáctico sobre este tema y similares.

Hoy en día, cada vez más empresas se ven involucradas por una u otra razón en la realización de Tests A/B con el fin de poder tomar mejores decisiones. Ya sean por cambios en UX de páginas web o Apps, cambios en segmentación o mensajes de campañas publicitarias, e incluso en distintas selecciones de modelos de Machine Learning, decidir que versión es mejor que otra conlleva una gran cantidad de tareas, que aquellos que lo intentaron, sabrán que no son fáciles. El objetivo de este articulo es poder darles una guía de pautas sobre distintos métodos de muestreo y evaluación para poder realizar experimentos que se adecuen de la mejor manera posible al desafío que tienen por delante. Para lograrlo revisaremos los siguientes temas:

Espero que luego de haber leído el articulo, tengan un mejor entendimiento de que no todos los tests o decisiones deben evaluarse de la misma manera, sino que existen alternativas más adecuadas a ciertos tipos de contextos, y que sepan el funcionamiento elemental de dichas alternativas.

Habiendo dicho eso, comencemos!

Historia de los Test A/B

1710: Primer Test de Hipótesis Publicado por John Arbuthnot en relación a la tasa de nacimiento de hombres vs la de mujeres. Primer versión de algo similar a los P-Values 1778: Pierre-Simón Laplace realizó otro test de hipótesis para el mismo tema utilizando P-values. Escribió las bases para lo que luego sería el teorema de Bayes. Finales del Siglo XIX: Comienzos del Test de Hipótesis “Moderno”, conocido como Frequentist. 2 enfoques:

1. Ronald Fisher: P-values, Continous Measure of Evidence, Hipótesis Nula. Sin noción de Potencia. https://www.adelaide.edu.au/
2. Neyman-Pearson: Nivel de significancia, Hipótesis Nula y Alternativa, Potencia, Error tipo 1 y tipo 2. http://www.nasonline.org/publications/biographical-memoirs/memoir-pdfs/neyman-jerzy.pdf

Errores tipo 1 y tipo 2

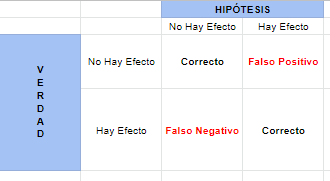
Al evaluar hipótesis (una alternativa y una nula) tenemos 4 resultados posibles

La idea general por Neyman y Pearson es que utilizando Tests de Hipótesis de esta manera, uno puede minimizar la frecuencia en la que realiza errores de tipo 1 y de tipo 2 dada una muestra fija. Esto se traduce a la siguiente receta:

• Cuanto más bajo el Error Tipo 1 y Tipo 2, mejor
• Para lograr eso, uno debe ‘pagar’ y en este caso, la moneda con la que se paga es el tamaño de la muestra.
• Por lo tanto para bajar alguna tasa de error uno debe: a) Aumentar la tasa del otro tipo de error b) Aumentar su presupuesto (tamaño muestral)

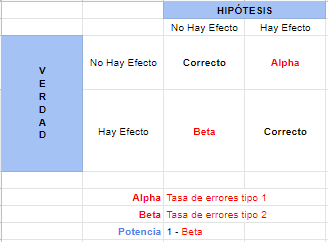
El enfoque de Neyman-Pearson es dar la mayor Potencia (el error tipo 2 más bajo) para una muestra de tamaño fijo y una tasa de Error Tipo 1 fija.

Por lo tanto, para calcular el tamaño muestral desde un enfoque Frecuentista necesitamos:

• Tasa de conversión o valor de la métrica objetivo esperado
• Desviación Estándar esperada
• Efecto Mínimo Detectable // Esto es sumamente importante ya que representa el problema de negocio. Busca contestar cuál es el efecto mínimo que requerimos encontrar para que represente un impacto práctico / significante en el negocio.
• Cuanto queremos controlar el Error Tipo 1 (Alpha)
• Cuanto queremos controlar el Error Tipo 2 (Potencia, 1-Beta)

Si me siguieron hasta acá sabrán entonces que cubrimos el método más conocido para diseñar experimentos. Peor no es el único! A continuación describiré otros métodos apoyándome en contestar por qué es que el método frecuentista no siempre es el ideal dependiendo del contexto.

¿Cuándo y por qué utilizar Bandits?

Quienes estuvieron prestando atención, habrán notado que el método frecuentista está centrado en disminuir lo más posible el Error Tipo 1. Esto resulta en experimentos no solo costosos en tamaño muestrál, sino que costosos en términos de riesgo para el negocio. Se centra en problemas donde queremos estar lo más seguros posibles de no estar ‘dañando’ el negocio, la experiencia, la métrica, etc. Son situaciones donde estamos dispuestos a dejar de lado oportunidades de de mejora si obtenerlas implica una probabilidad significativa de en verdad estar empeorando las cosas. Algunos ejemplos pueden ser rearmar el flujo de Checkout, un re diseño entero del sitio, cambios en el sistema de pricing, etc. Llamamos a este tipo de problemas como “No haga daño”

La buena noticia, es que no siempre nos encontramos en este tipo de situaciones! Existe otro tipo de problemas en los que cometer errores de Tipo 1 no es costoso para el negocio. Por ejemplo: Cambiar el copy de un anuncio, cambiar el titulo de una nota (el titulo de este articulo por ejemplo!), probar colores de botones distintos, o alternativas de UX para ciertas partes de un sitio, etc.

En estos casos, no hay un costo real considerable por tomar una acción que en verdad no mejore el negocio, la experiencia o la métrica. En cambio la prioridad es el costo de oportunidad de no estar dando una mejor experiencia. Por eso, llamamos a este tipo de problemas como “Dale nomas”. Cuando nos encontramos con este tipo de problemas, es que podemos considerar métodos de Bandits.

Estos son solo algúnos ejemplos de métodos de Bandits distintos:

1. Epsilon First (AB Testing)
2. Epsilon Greedy
3. Thompson Sampling
4. Pick por Potencia

Epsilon First

Si bien este método existe como una solución aproximada al problema de Bandits, podrán ver que es en verdad idéntico a como uno diseña un AB test frecuentista:

En este enfoque Epsilon First, primero se recolecta la información de cada variante, donde cada una tiene una probabilidad uniforme de ser seleccionada y se sirve aleatoriamente, y una vez recolectada la data se aplica un test de hipótesis para determinar al ganador. La versión ganadora luego se aplica al 100% de los usuarios.

El problema principal de este enfoque es que tiene un costo de oportunidad muy grande. Si una de las versiones es considerablemente inferior a otra, se le va a servir a los usuarios en la misma proporción que el resto, por todo el tiempo que se requiera para recolectar la información.

Epsilon Greedy

Una forma de disminuir ese costo de oportunidad mencionado anteriormente es con el método Epsilon Greedy. En este, se va intercalando el proceso de exploración y aprendizaje con el de Explotación. Para esto, se selecciona una tasa epsilon (por ejemplo 20%). De este 20% de usuarios es del cual vamos recolectando información de las variantes, sirviendo cada una de manera aleatoria con una probabilidad uniforme. Luego, la variante que mejor performa se aplica al 80% restante de los usuarios.

Ventajas de Epsilon Greedy:

1. Simple de utilizar y poco costoso
2. Muy efectivo
3. Poco afectado por estacionalidad

Sus desventajas son:

1. No es optimo (es difícil determinar que epsilon utilizar)
2. No mide la varianza del desempeño de las variantes
3. No tiene forma de determinar cuando dejar de correr el experimento
4. No tiene forma de determinar como ir disminuyendo la tasa de aprendizaje y aumentando la de explotación.

Modelos Adaptatívos

Se los llaman modelos adaptatívos porque la tasa de Exploración/Aprendizaje y la de Explotación no es fija, sino que va cambiando en el tiempo en base a algún criterio.

En este caso, nos centraremos en un tipo de modelo adaptatívo llamado Thomspon Sampling , inventado por William R Thompson en 1933. Este método de muestreo tiene bases en el teorema de Bayes en vez del test de hipótesis frecuentista que vimos anteriormente.

Y que es el Teorema de Bayes? Veamos un ejemplo:

Para entender mejor la imagen, lo que vemos es que el bebe tiene una idea aproximada que lo que está por comer es helado (Creencia a Priori), luego lo muerde (Evidencia) y obtiene una idea actualizada donde confirma que efectivamente lo que esta comiendo es helado (Creencia Posterior).

En síntesis, el Teorema de Bayes explica que mi creencia posterior sobre un hecho es explicada por el conjunto de lo observado (Evidencia) y mi creencia previa sobre el hecho.

Otra forma de verlo, es que el Teorema de Bayes intenta contestar la probabilidad de que mi hipótesis sea verdad dado los datos, basándose en la probabilidad de los datos dada mi hipótesis y la probabilidad de mi hipótesis en general. Esto supone una distinción muy importante respecto al método frecuentista de test de hipótesis, ya que el primero intenta contestar la probabilidad de que la hipótesis sea verdad, mientras que el segundo contesta cuan probable es lo observado en la data suponiendo que la hipótesis sea verdadera.

La crítica principal al método Bayesiano es que requiere esta “Creencia Previa” que muchas veces es subjetiva, y que para un mismo análisis, si se selecciona una Creencia Previa distinta, el resultado producido es distinto. Por eso la idea era sustituirlo por el método frecuentista, que quita esta subjetividad del análisis, aunque se puede argumentar que en el método frecuentista, todos los parámetros de diseño también son subjetivos (alpha, beta, MDE, etc).

Posteriormente, cuando Laplace demuestra el teorema central del límite, se suponía entonces que con gran volúmenes de datos, ambos métodos convergían a resultados similares, aunque se demostró que eso no siempre sucede.

Ahora que tenemos un mejor entendimiento del método Bayesiano, volvamos a los Métodos Adaptatívos para experimentación y el Thompson Sampling.

Como veniamos diciendo, el método de Thompson Sampling se basa en la base del Teorema de Bayes. Que significa esto? Que este método utiliza la probabilidad de que una variante sea mejor para decidir que variantes ir sirviendo a los usuarios.

El orden de procedencia es el siguiente:

1. Servir variantes de forma aleatoria
2. Seleccionar basado en la probabilidad de que esa variante sea la mejor
3. Aquella variante con la mayor probabilidad de ser la mejor es seleccionada más frecuentemente.

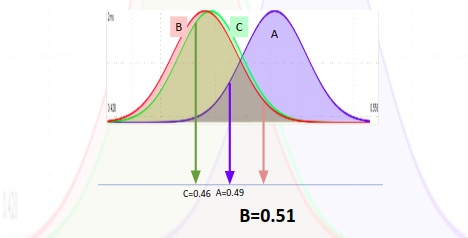
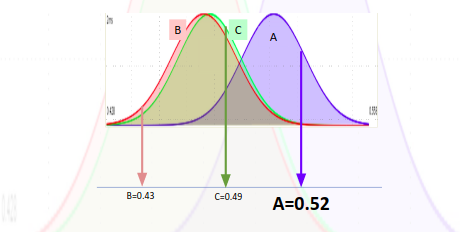
Veamos un ejemplo con un test donde nuestra métrica objetivo es la tasa de conversión, que sigue una distribución Beta con parámetros alpha (éxitos) y beta (fallas) , y donde tenemos 3 variantes que estamos probando, cada una con su respectiva distribución Beta.

Luego de haber servido cada variante de forma aleatoria un par de veces, podremos armar sus respectivas distribuciones Beta. Por lo tanto, al momento de decidir que variante servirle a un usuario, tomamos un valor aleatorio de cada distribución. En este ejemplo, la variante A obtuvo un valor de 0.49, la B de 0.51 y la C de 0.46. Dado que la B obtuvo el valor aleatorio más alto, procedemos a servir la experiencia B.

Y qué pasa luego de que servimos la experiencia? Bueno, resulta que si el usuario convierte (realiza la tarea objetivo en la que estamos interesados), vamos a ajustar el parámetro Alpha (éxitos) de la distribución Beta de la variante B sumándole 1. Pero en caso de que el usuario no termine convirtiendo, entonces ajustamos su parámetro Beta (Fallos) de su distribución. Como resultado, cada vez que servimos una variante, la distribución de la misma ira cambiando, y por lo tanto cambia su probabilidad de ser la mejor variante entre las 3.

Ahora un nuevo usuario ingresa al sitio, y el proceso comienza de nuevo:

Esta vez, la variante A obtuvo el mayor valor, por lo cual se servirá esta variante y se actualizaran sus parámetros acorde. Este método entonces aproxima la probabilidad relativa de que una variante sea la mejor, y las selecciona en base a dicha probabilidad. El proceso continúa hasta que decidamos un ganador.

Y como decidimos finalmente qué variante es la mejor? Bueno esto dependerá del problema que estamos intentando resolver, pero por ejemplo, podríamos decidir una que una variante es la mejor, cuando su probabilidad de ser la mejor es mayor o igual a 95%.

Puede que ya lo hayan notado, pero uno de los problemas que tiene este método, es que a diferencia del método frecuentista, Thompsom Sampling no tiene un tamaño muestrál fijo, ni un valor crítico donde terminar el experimento (excepto el que se decida a discreción). En los casos donde el cliente/gerente/dueño/etc requiera determinar si o si un ganador en un tiempo determinado, Thompsom Sampling no se adecua como herramienta.

Qué podemos hacer en estos casos? Si el problema en cuestión lo amerita podemos utilizar la Selección por Potencia.

Selección Por Potencia

La selección por potencia es un método estrictamente frecuentista, pero con una variante que a simple vista puede ser considerada controversial.

Para realizar una Selección por Potencia, debemos hacer lo siguiente:

1. Seleccionar una potencia deseada (1 - beta). Ejemplo: 0.95 o 95%
2. Seleccionamos un Efecto Mínimo Detectable.
3. Seleccionamos un Alpha

Hasta aquí todo es igual a un test de Hipótesis Frecuentista clásico, verdad? Pero, en este caso, el alpha que seleccionaremos es de 0.5 (no confundir con 0.05, que es el que se utiliza para una significancia del 95%)

Esto se traduce en que este experimento no tendrá ningún tipo de control sobre el Error Tipo 1, ya que al seleccionar un alpha de 0.5, o 50%, nuestra probabilidad de cometer un Error Tipo 1 es igual que aleatoria.

Entonces, calculamos nuestro tamaño de muestra necesario utilizando estos parámetros, recolectamos los datos, y seleccionamos aquella versión que haya dado el mejor resultado Así de simple! Pero se preguntaran cómo es que esto suele funcionar? Veamos un ejemplo realizando simulaciones asumiendo que el efecto es verdadero:

Para un experimento con estos parámetros vemos que necesitamos 4650 observaciones, es decir 2325 observaciones por variante (asumiendo 2 variantes). Para simular entonces calculamos una muestra de 2325 observaciones de A y 2325 de B, calculamos la tasa de conversión de cada una, luego calculamos la diferencia entre ambas (Tasa Conv B - Tasa Conv A). Este proceso lo realizamos 10 mil veces, por lo que tendremos un listado con 10mil diferencias entre la tasa de conversion de B y de A.

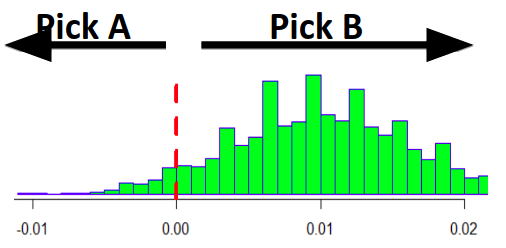
Si graficámos la distribución de estas diferencias, nos encontramos con llo siguiente:

Aquí podemos ver que la distribución está centrada en la diferencia real que establecimos (ya que las muestras que tomamos fueron de variantes A y B donde en verdad existía una diferencia de conversión) de 0.01 (0.05 de B menos el 0.04 de A). Pero lo interesante es que la probabilidad (area bajo la curva) de una diferencia mayor a cero, es de 95%!! El mismo valor que establecimos como potencia! Eso significa que si luego de tomar los datos de las muestras necesarios, seleccionamos aquella variante que tuvo una mejor tasa de conversión, el 95% de las veces estaremos seleccionando correctamente la versión que mejor performa.

Ahora, qué pasa con nuestro riesgo de cometer Error Tipo 1? Cuál fue el efecto de haber establecio un alpha de 0.5? Para eso, vamos a repetir esta simulación, pero ahora las muestras las tomaremos de 2 variantes que tienen la misma tasa de conversión de 0.4 (Por lo tanto, un experimento donde en verdad no hay efecto alguno):

Podemos ver que en este caso, la distribución de nuestros resultados (10 mil diferencias de Tasa de Conv B - Tasa de Conv A) se centra en 0, lo cual tiene sentido dado que pusimos tasas iguales de 0.04 para ambas variantes. Esto significa que en este caso, si luego de correr el experimento seleccionamos como variante ganadora aquella que tuvo la mayor tasa de conversión, estaremos seleccionando correctamente el 50% de las veces. Pero dado que en el contexto del problema, no nos interesaba controlar el riesgo de estar eligiendo una versión que pueda ser peor, este resultado no sería grave.

En resumen, realizar selección Por Potencia, nos permite ejecutar un experimento con tamaños muestráles ampliamente menores al que necesitaríamos si decidiéramos niveles de significancia altos (alpha = 0.05 o 0.01), pero en caso de haber efecto, estaríamos seleccionando la versión correcta el 95% de las veces, o el % de las veces que determinemos con la Potencia que decidamos. Comparemos entonces el mismo experimento con las 3 metodologías en las que nos enfocamos:

Como pueden ver, el Test AB clasico (con alpha de 0.05) requiere una muestra de 18600 observaciones totales, mientras que Thompsom Sampling obtiene el mismo resultado con solo 4800, y finalmente, la Selección por Potencia necesita solo de 4650 observaciones.

Conclusión

Si bien nunca hay que olvidar los supuestos que uno debe respetar al seleccionar cualquier metodología estadística para realizar Test de Hipótesis, espero que con esta lectura hayan podido apreciar que dependiendo el problema, hay metodologías que permiten resolver los Tests de forma menos costosa, es decir, con menos tiempo de recolección de datos y por lo tanto mayor tiempo de explotación de los resultados.

Algunos casos donde metodologías como Thompsom Sampling o Selección de Potencia suelen ser más idóneos que el Test de Hipótesis frecuentista clásico:

1. El aprendizaje es perecedero (Cuanto más se tarda en aprender, menos valor tiene dicho aprendizaje)
2. Procesos Always-On (Tests sobre sujetos que correrán constantemente, como anuncios de campañas, modelos de Machine Learning, etc)
3. Decisiones Complejas (Como por ejemplo estar actualizando constantemente un modelo de ML)

Espero que con lo mencionado en este articulo, se animen a realizar más Test de Hipótesis, con distintos métodos de muestreo y evaluación y que lleguen a sus propias conclusiones sobre que metodologías se adecuan más a sus casos de uso y problemas de negocio!

---

Gracias por leer mi blog!

Si te gustó lo que leiste te invito a que te sumes al newsletter para recibir un mail semanal con el nuevo contenido y novedades. O podes apoyarme con su desarrollo invitandome un cafe :) Muchas gracias!

Subscribirse