Test Bayesiano vs Frecuentista
Es importante entender las diferencias fundamentales entre ambos, en especial que cada metodología busca contestar preguntas distintas, y que por eso muchos argumentos brindados por los vendors sobre porque uno es mejor que el otro son erróneos
Hace ya un tiempo que hay una tendencia en internet sobre una metodología distinta para experimentación, que para este artículo denominaremos “Test AB Bayesiano”. Digo distinta porque por lo general, casi todas las empresas que ofrecían herramientas y calculadoras para Tests AB se basaban en el método frecuentista, también conocido como Null Hypothesis Significance Testing, al que me voy a referir cómo NHST en este artículo.
El problema que encuentro, es que casi todos los vendors que ofrecen esta metodología (Google Optimize, VWO, AB Tasty, Dynamic Yield y más) suelen comunicar las ventajas respecto al NHST como abrumadoras, apalancando se en un pequeño subconjunto de argumentos, muchas veces mal interpretados.
Por lo tanto con este artículo me propongo:
- Marcar las características elementales de NHST y Test AB Bayesiano
- Dar contexto de porque el Test AB Bayesiano se puso de moda en los vendors más importantes
- Demostrar que cada uno busca contestar distintas preguntas, y por lo tanto no son sustitutos uno del otro
- Desmitificar alguno de los argumentos erróneamente comunicados a favor de Test AB Bayesiano
Es importante que sepan que yo particularmente no estoy más a favor de uno que del otro, e intentaré plasmar esa opinión lo más objetivamente posible en el contenido a continuación. De lo que sí estoy a favor, es de que haya un conocimiento claro sobre las distintas metodologías de experimentación y creo que con el fin de lograr un mayor atractivo y por lo tanto más ventas, la comunicación sobre estos temas está sesgada y siendo poco justa.
Por lo tanto, comencemos dando contexto a esta discusión.
Contexto
Para quienes estén familiarizados con NHST, sabrán que realizarlo correctamente requiere realizar un test de potencia previo en base a ciertos parámetros, que nos devuelve una cantidad de observaciones mínimas para que nuestro experimento tenga validez respecto a esos parámetros. Por lo tanto, para ciertos diseños experimentales, ese requisito es muy limitante dado que en general nosotros experimentamos con el tráfico que nuestro sitio recibe, y no podemos generar más visitantes de un día para el otro. Por lo tanto cuando realizamos un test de potencia con nuestros parámetros ideales y nos da que necesitamos más observaciones de las que podemos obtener en un tiempo considerable, nos vemos limitados a decidir no correr el experimento, o a sacrificar algún aspecto / parámetros de nuestro diseño experimental por otro menos ideal pero que sí podamos realizar.
Por otro lado, además de cumplir con las observaciones necesarias, debemos obedecer de no querer frenar el experimento cuando vemos un resultado que nos interesa (por ejemplo un p-value < 0.15), dado que frenar el experimento bajo esas condiciones, algo que entra en lo que se denomina Optional Stopping, invalida el control de los parámetros que decidimos en el test de potencia, a excepción de que hayamos hecho un diseño experimental que sí tenga en cuenta esa posibilidad (como test secuenciales) pero que por lo general no son lo que más se aplica.
Y por último, si realizamos el diseño experimental correcto, respetamos las reglas que nos impone, y concluimos el experimento, el mismo nos devuelve como resultados un p-value y un intervalo de confianza, que son dos valores que mucha gente malinterpreta y considera confusos de entender.
Entonces aparece una nueva alternativa. Una metodología que dice no necesita correr por una cantidad mínima de días o juntar una cantidad mínima de observaciones, que se puede frenar en cualquier momento y aún así mantener resultados válidos, y que su resultado es más fácil de interpretar que un p-value. ¿Suena tentador verdad?
Esta alternativa es lo que se denomina Test AB Bayesiano. Y los argumentos que mencioné recién son una simplificación bastante certera de los mismos argumentos que usan los vendors mencionados anteriormente para convencerte de cambiar a esta metodología.
Pero el truco está en que al cambiar de una metodología a otra, se está cambiando la pregunta o problema a resolver, y por lo tanto esos beneficios dejan de ser contrastables a las limitaciones del NHST, dado que apuntan a objetivos distintos.
Veamos por qué.
NHST
El NHST entiende a la probabilidad como una frecuencia de sucesos, por eso se llama estadística frecuentista. Concretamente, el suceso al que hace referencia un NHST es al error. ya sea el error de tipo 1 o el error de tipo 2. Lo que tiene como objetivo un NHST bien hecho es controlar la frecuencia de veces que estaríamos cometiendo alguno de esos errores. En el caso del p-value, el mismo debe interpretarse como: Si la hipótesis nula es verdad, un valor del tamaño que observamos o mayor, es esperable un p-value por ciento de las veces. Por lo tanto, si decidimos rechazar la hipótesis nula en pos del valor que observamos, estaríamos cometiendo un error de tipo 1 un p-value por ciento de las veces.
Lo mismo con el error de tipo 2 y por lo tanto con la potencia de un test. Como podrán ver, el NHST busca controlar por esos errores, independientemente de cual sean los valores de su hipótesis, sea que el efecto es menor a 0, a 10, mayor a 20, o que sea exactamente 5, da igual. La dificultad reside en que si uno está intentando detectar efectos muy pequeños, o que la varianza de la métrica a evaluar es muy grande, o el nivel al que uno quiere controlar dichos riesgos es muy alto, entonces la metodología requiere muchas observaciones para poder discernir ese control. No es lo mismo querer estar seguro de que la probabilidad de equivocarse es solo un 5% que un 50%, y tampoco es lo mismo querer estar seguro que un efecto es de al menos el 15%, que del 0,015% con el mismo nivel de seguridad.
Lo que no nos dice un NHST es cual es la probabilidad de la hipótesis por ejemplo. No nos dice cuán probable es que haya un efecto positivo, ni nos dice cuán probable es que el efecto esté entre tal número y tal otro. No confundir esto úlltimo con el intervalo de confianza, dado que el intervalo de confianza (por ejemplo al 95%) de un NHST nos dice: si uno calcula un intervalo de confianza al 95% repetidamente en varios experimentos iguales y válidos, en promedio el 95% de las veces el rango de confianza va a contener el efecto real del tratamiento. Ven? De nuevo aparece lo de “repetidamente en varios experimentos”. Porque seguimos en el marco de la frecuencia esperada de lo observado. Seguimos en estadística frecuentista.
Hay muchos otros detalles que podemos mencionar sobre NHST, pero lo anterior es lo mínimo que creo necesario para que puedan continuar con este artículo. Quienes les interese saber más pueden aventurarse a esta otro artículo.
Test AB Bayesiano
La estadística bayesiana no es más nueva que la frecuentista. De hecho existe desde antes, y la disputa entre ambas metodologías continúa hasta el día de hoy, donde ahora se enfrentan en el ámbito de la experimentación online.
Los Test AB Bayesianos interpretan la probabilidad no como una frecuencia de sucesos, sino como una comparación entre qué cosa es más probable que la otra. En este caso la “cosa” en cuestión sería la hipótesis. Entonces como resultado por lo general obtenemos un coeficiente de cuánto más probable es una hipótesis que la otra, y a su vez una distribución de posibles valores del efecto.
Como hace la estadística Bayesiana para obtener estos resultados? Se basa en el Teorema de Bayes donde:
Acá la P(H|D) es la probabilidad de la hipótesis en cuestión dada la data, P(d|H) es a probabilidad de la data observada dado la hipótesis (también conocido como Likelihood), la P(H) es la probabilidad de la Hipótesis en cuestión (lo que se conoce como Prior) y P(d) es la probabilidad de los datos.
En un contexto de experimentación online, P(d|H) o Likelihood es simplemente la distribución de los datos observados. Por ejemplo cuando nuestra métrica a observar es un promedio, nuestro likelihood sigue una distribución normal (Venta por usuario promedio, Páginas vistas por usuario promedio, etc) y cuando es una proporción (Tasa conversión, CTR) sigue una distribución Bernoulli. A su vez, el prior corresponde a nuestras creencias previas sobre la métrica. Por ejemplo, qué valores creemos que puede tomar el CTR o el ticket promedio. También se puede asignar un prior a la distribución del efecto, por ejemplo creer que el efecto tiene que estar entre tal y tal número.
Por lo general los priors son algo que se puede calcular con data histórica, y algún otro ajuste de flexibilidad o información del negocio o del tratamiento. El poder incluir información subjetiva al diseño experimental es uno de los puntos que más destacan de la metodología Bayesiana, ya que es la herramienta que le permite “agilizar” los resultados, es decir, requerir menos observaciones.
No es mi objetivo en esta ocasión hacer un análisis técnico super profundo de esta metodología, pero sí que entiendan como los vendors mencionados anteriormente la utilizan para Tests AB en experimentación online.
La metodología bayesiana para Tests AB por lo general es la siguiente:
- Seleccionamos una distribución “Prior” para la métrica que vamos a evaluar, que puede ser la misma para el control (C) y el tratamiento (T) o pueden ser Priors distintos.
- Recolectamos los datos de cada variante, y ajustamos nuestros respectivos Priors con la data nueva observada (como se hace esta actualización dependerá de la distribución Prior seleccionada y de la distribución real de los datos observados)
- Ahora que tenemos dos distribuciones actualizadas (tratamiento y control), obtenemos de estas distribuciones N observaciones aleatorias, por ejemplo, 1 millón de muestras aleatorias de cada distribución (que normalmente se realiza con Simulaciones Monte Carlo)
- Comparamos el millón de muestras del tratamiento con el del control, y calculamos el porcentaje de veces que las muestras de tratamiento fueron mayores que las del control, y la diferencia entre cada columna, creando así una nueva columna que representa el “Efecto” (T - C).
- Repetimos el punto 3 y 4 con cada dato nuevo que vamos obteniendo
- Evaluamos la distribución de la columna Efecto, calculamos la probabilidad de que el efecto sea mayor a 0, el intervalo de valores con 95% de probabilidad de suceder, y alguna función de pérdida y frenamos el experimento cuando se cumpla alguna condición que nos interese.
Por lo tanto, de la misma forma que con los test frecuentistas debemos seleccionar criteriosamente nuestros parámetros alpha, beta y efecto mínimo a detectar, acá debemos seleccionar nuestras distribuciones priors para tratamiento y control, y alguna regla para decidir cuando efectivamente declaramos que una versión “ganó” o es mejor.
Pero no tuvimos que realizar un test de potencia, ni hay presente una cantidad mínima de observaciones, de la misma forma que no estamos mencionando en ninguna parte el error tipo 1 ni error tipo 2. Es porque la metodología bayesiana no controla por este tipo de riesgos, no son parte de sus cálculos en ningún lado. Su enfoque es contestar cuán probable es algo dado los datos observados (likelihood) y mi creencia previa sobre los datos observados (prior). Y cómo no requieren un tamaño muestral mínimo, cuando concluír un experimento Bayesiano queda a criterio del experimentador, aunque hay varios métodos conocidos de los cuales elegir.
Diferencias clave
Espero que con lo mencionado anteriormente, tengan una imágen clara de que intentan responder ambas metodologías. Eso es importante, porque al tener claridad sobre eso, se vuelve evidente que buscan responder preguntas complementante distintas, y que por lo tanto argumentar que una es “mejor” que la otra no tiene sustento sin el contexto del problema.
Pero por si alguno aún tiene dudas, voy a listar algunas diferencias importantes:
- El método NHST pertenece a la metodología frecuentista, y busca controlar la frecuencia de cometer errores (en este caso falsos positivos y falsos negativos) y de poder detectar efectos de determinado tamaño (potencia). Mientras que los Tests AB Bayesianos buscan responder qué valores de efecto son más probables o cuan más probable es que una versión sea mejor que la otra, dada los datos observados y la información subjetiva que elegí a priori.
- El NHST requiere de determinadas cantidad de observaciones para asegurar la correcta validez de sus resultados, por lo tanto juntar esas observaciones es lo que determina cuando debe parar un experimento. Los Tests AB Bayesianos no tienen esta condición, por lo que cuando parar el experimento depende de alguna regla establecida a criterio del experimentador, sea por observaciones o por alguno de los outputs de esta metodología.
- El NHST compara el valor estadístico observado con todos los valores posibles (aunque no hayan sido observados con los datos) para obtener sus resultados. El Test AB Bayesiano solo tienen en consideración los valores observados durante el experimento.
Argumentos mal comunicados
A continuación iré detallando con su respectiva fuente, algunos argumentos que utilizan los vendors para comunicar las ventajas de los Test AB Bayesianos sobre NHST, que dado lo explicado en la sección anterior puede que detecten porque en verdad no son así. De todas formas explicaré porque en cada argumento.
Google Optimize: Los métodos bayesianos nos permiten calcular probabilidades directamente, para responder mejor a las preguntas que los comerciantes actualmente tienen (en lugar de proporcionar p-values, que pocas personas entienden realmente) https://support.google.com/optimize/answer/7405543
VWO dice: “Ofrecemos métricas fáciles de digerir junto con recomendaciones para que puedas dejar de buscar la definición de p-value o verificar la significancia estadística, y sólo te concentres en cuáles deben ser tus próximos pasos.” https://vwo.com/why-us/technology/bayesian-statistics/
Dynamic Yield: Aunque no estamos profundizando en los detalles, se puede ver inmediatamente que el motor bayesiano proporciona respuestas a preguntas más directas como: ¿Cuál es la probabilidad de que A sea mejor que B? (contrasta esto con el p-value mencionado anteriormente) https://www.dynamicyield.com/lesson/bayesian-testing/
Ninguno brinda ejemplos de las preguntas que los comerciales actualmente tienen, pero asumo que se refieren a que a los comerciales les interesa solo saber que versión es más probable que tenga un efecto positivo (si Landing A o B, anunció A o B). Pero eso asume que a los comerciales no le interesan decisiones que puedan tener riesgos más altos, como modificar el sistema de pricing de sus servicios web, donde cometer un error de tipo 1 puede ser altamente riesgoso y perjudicial. O cambiar algún elemento de la infraestructura del sitio, o del funnel de checkout, etc. Además, asume que la interpretación del resultado es “la probabilidad de que variante A sea mejor que B” cuando en verdad la interpretación correcta es “la probabilidad de que la variante A sea mejor que B dada la data observada y la información adicional que haya utilizado para mis priors”
Por otro lado, si los p-values son difíciles de entender, difíciles en comparación con que? Porque en los Test AB Bayesianos, los comerciales deben elegir una distribución que modele sus creencias sobre el comportamiento de la métrica o del efecto (recuerden, el Prior es un elemento de esta metodología) y el modelo seleccionado puede tener repercusiones sobre el resultado. Me cuesta ver de qué manera se está reemplazando algo “difícil” por algo más “fácil”.
VWO: Usted no tiene que preocuparse por tomar las decisiones equivocadas basadas en menos datos. Tus resultados son válidos siempre que los mires. https://vwo.com/why-us/technology/bayesian-statistics/
Google Optimize: Dado que utilizamos modelos diseñados para tener en cuenta los cambios que se producen en los resultados a lo largo del tiempo, siempre es posible consultar los resultados. Nuestras probabilidades se perfeccionan continuamente a medida que recopilamos más datos. https://support.google.com/optimize/answer/7405543
AB Tasty: Puedes comenzar una prueba sin tener un tamaño de muestra definido de antemano. En su lugar, simplemente se inicia la prueba y tan pronto como se identifica un resultado significativo, se puede utilizar. https://www.abtasty.com/blog/bayesian-ab-testing/
Para entender porque esta declaración de que los resultados son válidos siempre que los mires, o que podes frenar el experimento en cualquier momento, es importante entender válidos respecto a que. Dado que se están comparando con los NHST, uno podría creer que significa que son válidos respecto a controlar por los errores de tipo 1 o 2. Eso es imposible dado que la metodología bayesiana en ningún momento busca controlar esos errores, así que decir que una metodología mantiene la validez respecto a la otra en algo que la primera no se propone controlar, es inválido.
Entonces a qué validez se refiere? Resulta que la interpretación de un Test AB Bayesiana es siempre válida respecto a sus propios resultados, porque trabaja con la data observada más los priors que seleccionemos. Esto significa que si yo miro los resultados hoy y veo una “Probabilidad de que A sea mejor que B del 80%” quiere decir exactamente que “Dada la data observada y los priors seleccionados, la probabilidad de que A sea mejor que B es del 80%”. Si mañana ese número cambia a 60%, la interpretación sigue siendo válida. Ese es el tipo de validez al que se refieren.
Para más detalle sobre esto pueden consultar este post que ejemplifica muy bien este asunto remarcando que el Test AB Bayesiano no promete un control sobre el error de tipo 1: Link
En contraste no podríamos hacer lo mismo con NHST porque estaríamos inflando la frecuencia de cometer un falso positivo. La interpretación de un NHST solo es válida si se cumplió el diseño experimental correcto para poder controlar por los parámetros seleccionados.
Ahora que establecimos a qué validez se refiere el Test AB Bayesiano, y cómo se diferencia de la del NHST, creo importante aclarar dos elementos importantes sobre el supuesto beneficio de parar el experimento en cualquier momento.
-
Cuando parar un experimento de Test AB Bayesiano, como mencione anteriormente, queda a criterio del experimentador y sus objetivos. Sin embargo las opciones más frecuentes en experimentación online son: A. Probabilidad de ser mejor : La probabilidad de que A sea mayor que B B. Función de pérdida: Hay muchas, una común es el efecto esperado cuando B es mayor que A, que se interpreta como “cuánto pierdo si elijo A pero en verdad B era mejor” C. Intervalo de alta densidad: Que tamaño de efectos posibles pertenecen al intervalo del 95% de probabilidad. Si este intervalo excluye un determinado rango, freno el experimento a favor de tal variante.
-
La elección de bajo que criterio frenar el experimento viene con determinados costos: A. Si bien a esta metodología no le interesa controlar por falsos positivos, la elección de estos criterios tiene incidencia directa en cuán alta es la probabilidad de obtener falsos positivos. B. También la precisión de la estimación de los efectos es afectada por el criterio se utiliza para frenar el experimento.
John Kruschke, el autor de Doing Bayesian Data Analysis explora los efectos de distintos criterios para frenar el experimento en ambos factores y pueden encontrar sus resultados acá: Link
Y por último sobre este tema, si los resultados son siempre válidos, porque es que Google Optimize, VWO y Dynamic Yield aconsejan o exigen correr los experimentos al menos 1 o 2 semanas? La respuesta es para poder controlar por la variabilidad de resultados por efectos de estacionalidad, y para un test de NHST aconsejaría lo mismo, sin embargo creo que sería justo que eso se mencionara en las comparaciones que realizan.
Por lo tanto, si, la interpretación de un Test AB Bayesiano es válida en cualquier momento del experimento, pero eso no quiere decir que sus conclusiones sean las deseadas o las más óptimas.
El último argumento que me interesa mencionar es quizá el más complejo y a su vez el más importante, y tiene que ver con la elección del Prior, que para los que son nuevos en este tema entiendo que es un concepto difícil de comprender.
Recuerden que les dije que el prior supone una ventaja de la metodología bayesiana, porque nos permite incluir información externa al experimento, ya sea en base a data histórica de experimentos pasados, del comportamiento esperado de la métrica, o temas del negocio. Y que hacer eso permite obtener resultados más ágilmente, dado que es como arrancar el experimento con un camino marcado, en vez de a oscuras.
Teniendo eso en cuenta uno esperaría que las plataformas que utilizan esta metodología permitiran que el usuario decidiera sobre sus priors, pero ese no es el caso:
Google Optimize: No te permite establecer los priors en ninguna parte, y ellos mismos dicen: “Con respecto a los ganadores y las tasas de conversión, hacemos todo lo posible para usar piors no informativos… priors con la menor influencia posible en los resultados del experimento.” https://support.google.com/optimize/answer/7405544?hl=en
Dynamic Yield también utiliza priors no informativos (Beta 1,1 para proporciones y una Gamma K,T para Venta por usuario) https://support.dynamicyield.com/hc/en-us/community/posts/360012753898-Prior-distributions- (requiere estar logeados)
AB Tasty y VWO por lo visto no tienen opción de setear los priors manualmente, y no encontré documentación sobre que priors utilizan.
Entonces cómo puede ser que un elemento tan importante de esta metodología, y sobre el cual se basan argumentos como la agilidad respecto a NHST, estén tan poco informados y el usuario no tenga control sobre ellos?
Esto se vuelve un problema porque como dijimos, la interpretación del resultado de estos tests es: “la probabilidad de que A sea mejor que B dada la data observada y el prior utilizado”. Y para algunos casos no tenemos información sobre qué priors se utilizaron, y para los que sí, igual no podemos elegir nuestros propios priors que hagan sentido para nuestro análisis.
Esto como usuario me deja creyendo que en verdad los Tests AB Bayesianos son sólo más “fáciles” que los NHST, cuando le quitamos la complejidad al usuario de tener que elegir quizá el aspecto más importante de su metodología, que es el prior. Algunos podrán argumentar que esta decisión es porque dada una cantidad suficiente de observaciones recolectadas, los priors elegidos dejan de tener peso respecto al resultado. Pero eso igual depende del prior seleccionado, Cuanto más restrictivo sea el prior que seleccione, más va a tardar eso en suceder. Pero no encontré aún estudios que determinen a partir de qué tamaño de observaciones eso sucede y su impacto en los Tests AB Bayesianos, por lo que esconder esa información al usuario tampoco me parece justo.
El equivalente en NHST sería que no puedas elegir tu alpha ni tu beta, y por lo tanto yo te diga si tu resultado es significativo o no sin que vos sepas qué medida estás controlando los falsos positivos o la potencia.
Conclusión
Espero que con todo lo mencionado anteriormente, entiendan que las dos metodologías son extremadamente distintas porque desde su naturaleza buscan contestar preguntas distintas. Creo que ambas tienen su lugar en la experimentación online, y que de hecho se complementan, pero solo si se tiene claro el objetivo y contexto de cada experimento. Los argumentos y promesas que ofrecen los vendors sobre la metodología bayesiana no resisten una evaluación estricta respecto al contexto dado que simplifican toda la metodología a solo un aspecto, le quitan al usuario la posibilidad de utilizarla correctamente y se comparan con el NHST en puntos que no son comparables.
Hay casos donde controlar riesgos de errores es más importante, y casos donde poder modelar el comportamiento o conocimiento previo para poder tener una estimación rápida y precisa de un efecto sea el objetivo. Por eso es que nadie se salva de tener que, frente a un problema o incertidumbre, enmarcar la toma de decisiones, y elegir una metodología que se adecue a ese marco, sea frecuentista o bayesiana, y ejecutar la misma de la forma más correcta posible, con sus pros y contras.
Gracias por leer mi blog!
Si te gustó lo que leiste te invito a que te sumes al newsletter para recibir un mail semanal con el nuevo contenido y novedades. O podes apoyarme con su desarrollo invitandome un cafe :) Muchas gracias!
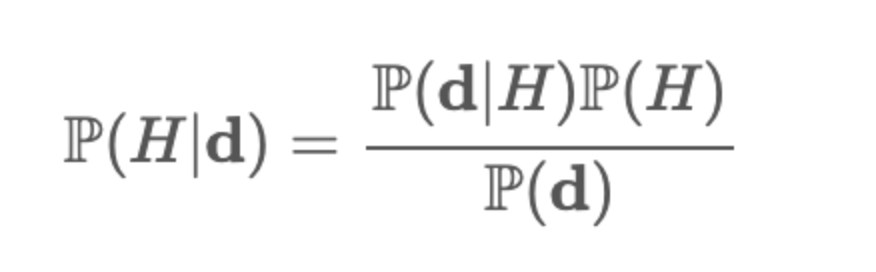


Share this post
Twitter
Facebook
Reddit
LinkedIn
Email