Errores frequentes en Tests AB clásicos
Muchos equipos suelen cometer errores a al hora de hacer A/B Tests. Aquí encontraran una explicación de los que yo considero más frecuentes y sus efectos en la validez del experimento
En mi primer posteo, que pueden encontrar acá , mencioné algunos errores comunes que los equipos cometen a la hora de hacer A/B tests. En este post voy a profundizar en algunos de estos errores. Mi objetivo es que ganen un mejor entendimiento de por qué el error es en efecto un error, y de qué forma altera o invalida la interpretación de resultados de ese experimento.
TL:DR
Los 4 errores más frecuentes y que hay que tratar de evitar son:
Malinterpretar los p-value: Los p-values no nos dan probabilidades respecto a la hipótesis que queremos probar, sino que son un resultado de todo el proceso experimental que diseñamos. Hay muchas formas de malinterpretarlo, por lo que es importante tener un correcto entendimiento del mismo.
No reportar intervalos de confianza: Los intervalos de confianza nos permiten identificar posibles tamaños de efecto que aún no tenemos evidencia para rechazar. Nos dan un mejor entendimiento del tamaño del efecto sobre la hipótesis nula. No reportarlos nos deja con una mirada limitada del procedimiento experimental.
No realizar el test de potencia: Para que nuestro experimento controle por los riesgos y efectos que nos interesa controlar, debemos realizar un calculo de potencia para saber cual es el tamaño muestral necesario. No recolectar la muestra necesaria invalida las interpretaciones que hagamos sobre los resultados, y nos puede llevar a conclusiones erroneas.
Concluir el experimento de forma anticipada: Objetivos de negocio o un mal entendimiento de los p-values nos puede llevar a querer concluir experimentos cuando alcanzan significancia, sin recoelctar las observaciones necesarias. Esto invalida los resultados y aumenta la probabilidad de estar obteniendo un falso positivo.
Interpretar erróneamente el p-value
Muchas veces uno se encuentra con la siguiente situación: Se decidió que se quería hacer un experimento. Se crea el grupo de tratamiento y el grupo de control, se espera un tiempo determinado, y después se calcula la significancia de la métrica objetivo.
Para un ejemplo supongamos un caso donde la métrica objetivo es una tasa de conversión, y que los grupos son visitas a un sitio web. Durante una semana, se divide el tráfico al sitio web y al terminar la semana obtenemos lo siguiente:
| Grupo | Visitas | Tasa de Conversion |
|---|---|---|
| Control | 1000 | 5% |
| Variante | 1000 | 5.55% |
Entonces, el equipo va, y usando cualquier calculadora de significancia (hay muchas gratuitas en internet), obtiene un p-value de 0,28.
¿Que significa eso? Quiero que se detengan un segundo, y si esta situación les es familiar, piensen que responderían si alguien les pregunta qué significa un p-value de 0,28.
La respuesta correcta es que con la información que tenemos, ese p-value no significa nada. El p-value en estricto rigor es la probabilidad de que el estadístico de prueba elegido hubiera sido al menos tan grande como su valor observado si todas las suposiciones del modelo fueran correctas, incluida la hipótesis de prueba.
Pero como verán, en nuestro ejemplo no tenemos ninguna hipótesis! Ni nula ni alternativa, nada. Entonces nada puede interpretarse de un p-value obtenido de esa manera.
Ahora, si cuando les pregunte que significaba un p-value de 0,28, habían llegado a una respuesta, distinta a la que mencioné recién, es probable que hayan caído en alguna de las interpretaciones erróneas del p-value que listare a continuación:
- “El p-value es la probabilidad de que la hipótesis nula sea verdadera”: Esto es incorrecto porque desde el comienzo, el p-value ya asume, dentro de muchas cosas, que la hipótesis nula ES verdadera. Recuerden, el p-value solo indica el grado en el que la data observada se adecua a los supuestos de nuestro test, uno de ellos, la hipótesis nula. Por lo tanto, a más alto el p-value (cercano a 1), más se adecua el valor observado a nuestra hipótesis nula, y a más bajo el p-value (cercano a 0), menos se adecua nuestra hipótesis nula.
- “Un resultado significativo (p-value menor a 0,05 por ejemplo) significa que la hipótesis nula es falsa”: Esto no es cierto, porque como venía diciendo, un p-value pequeño solo nos indica que la data observada es inusual, dada nuestra hipótesis nula y asumiendo que todo el experimento y sus supuestos son válidos. Puede pasar que el p-value obtenido haya sido pequeño no porque la hipótesis sea falsa, sino porque violamos alguno de los supuestos.
- “Un resultado no significativo (p-value mayor a 0,05 por ejemplo) significa que la hipótesis nula es verdadera”. Mismo caso que el punto anterior, pero al revés. Un p-value más cercano a 1 solo nos indica que la data observada no es inusual bajo esta hipótesis. Una variante de esta interpretación es creer que un resultado no significativo es creer que no hay efecto. En estos casos el problema pudo venir de un diseño sin la potencia suficiente para detectar determinado efecto, algo que explico más adelante.
- “El p-value representa la probabilidad de obtener el valor que observamos, asumiendo que la hipótesis nula es verdadera”. Esto tampoco es cierto porque, si vuelven a la definición del p-value que puse antes, fijense que dice que es la probabilidad de que el valor observado sea AL MENOS de ese tamaño. Pero ese p-value tambíen cubre todos los tamaños mayores al que observamos.
Estas son solo algunas de las interpretaciones erradas sobre p-values, pero en mi experiencia las más frecuentes.
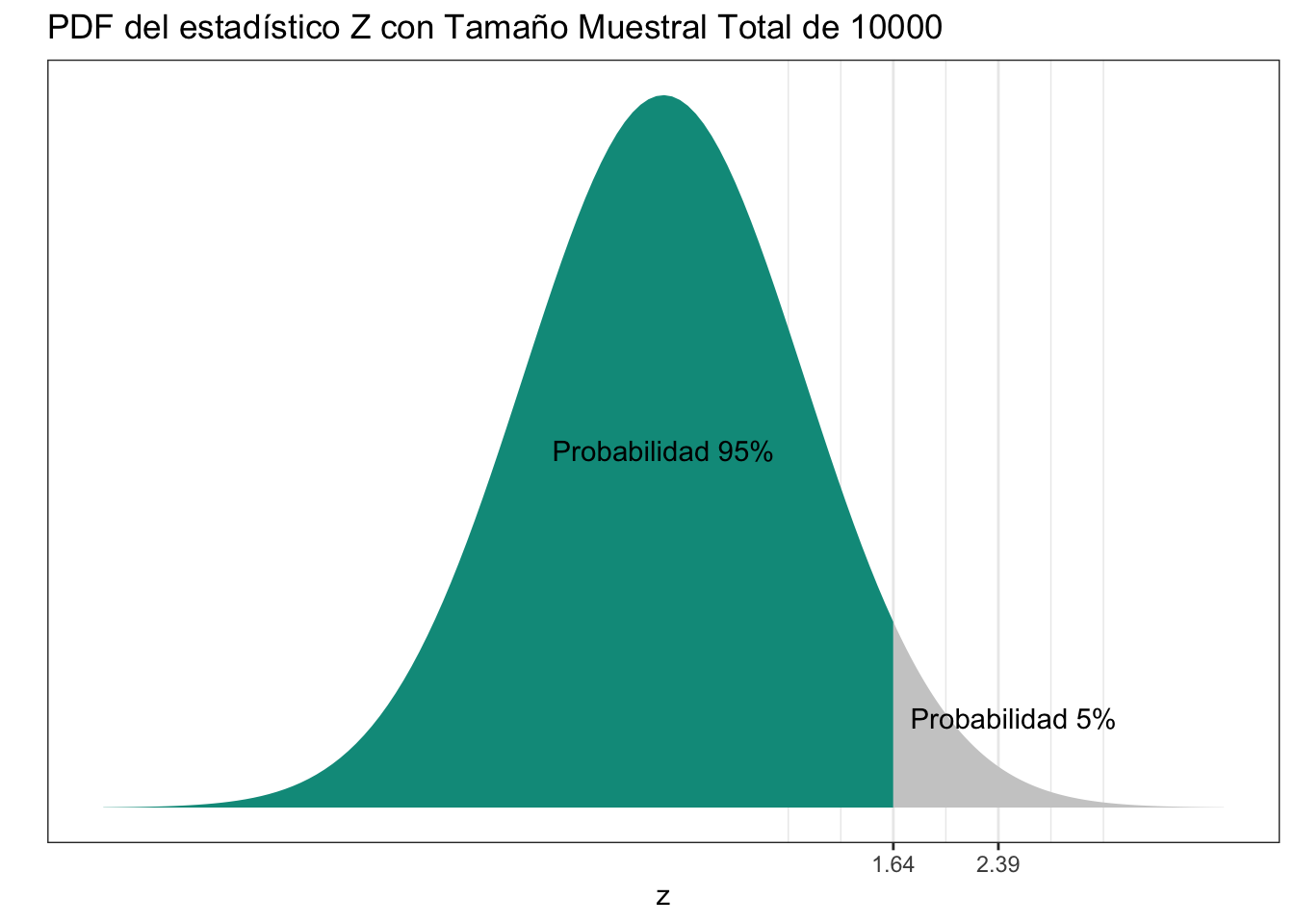
Visualmente, un p-value representa lo mostrado en el gráfico anterior. En ese ejemplo, asumiendo que la hipótesis nula es verdadera, hay un 95% de probabilidad de que el estadístico de prueba observado se encuentran en el área verde, y un 5% de probabilidad que se encuentre en el área gris. Cuando decimos que un test es “significante” al 5%, estamos diciendo que el valor observado se encuentra efectivamente en el área gris. Cuando modificamos la significancia, el alpha, de 5% a 1% por ejemplo, lo que estamos haciendo es achicar el área gris, moverla más hacia la derecha (en los casos de tests de una sola cola)
Otra equivocación muy frecuente en A/B tests de este tipo es reportar solamente significancia y los p-values (estén estos siendo bien interpretados o no).
No reportar intervalos de confianza
¿Por qué esto se puede considerar un error? Porque los p-values por sí solos no nos ayudan a entender el posible tamaño del impacto de nuestro experimento. Aquí es donde entran los intervalos de confianza.
Un intervalo de confianza es un rango de valores “atados” a un nivel de confianza, que suele ser el mismo que se utilizó para determinar significancia, por ejemplo 95% (1 - alpha con alpha = 0,05). Lo que caracteriza a un intervalo de confianza es la siguiente propiedad: si uno calcula un intervalo de confianza al 95% repetidamente en varios experimentos iguales y válidos, en promedio el 95% de las veces el rango de confianza va a contener el efecto real del tratamiento.
Pero qué significan los valores que se encuentran en un intervalo de confianza? Estos valores son aquellos tamaños de efecto posible que nuestro procedimiento experimental no tiene la confianza suficiente para rechazar. O se puede ver a la inversa, y pensar que si yo eligiera un valor fuera del intervalo de confianza, como parámetro para la hipótesis nula, la data observada no da evidencias para ese valor o esa hipótesis.
Vamos con un ejemplo:
| Grupo | Visitas | Tasa de Conversion |
|---|---|---|
| Control | 10000 | 5% |
| Variante | 10000 | 6% |
Con una alpha = 0,05 para un test de una sola cola, donde la hipótesis nula es que la diferencia de la tasa de conversión entre grupos es 0 o menos, obtenemos un p-value de: 0,001. Cómo ya aprendimos que no hay que reportar sólo los p-values, procedemos a calcular el intervalo de confianza, que nos devuelve lo siguiente:
IC = [0.01, +∞)
Entonces ¿qué nos dice este IC? Que los datos observados bajo el procedimiento experimental que hice no me dan evidencia para creer en una hipótesis nula donde esperaría que la diferencia entre las tasas de conversión sea menor a 0.01. Acuérdense, que partimos con una hipótesis nula donde la diferencia entre las tasas de conversión se suponía menor o igual a 0, y ahora tenemos evidencias de que la hipótesis nula no debiera ser menor o igual a 0,01. Si hiciéramos el experimento con los mismos datos , y una hipótesis nula de diferencia menor a 0.01, es muy probable que la rechazamos nuevamente (que no quiere decir que valores menores sean imposibles)
La interpretación errónea más frecuente de los intervalos de confianza suele ser:
- “El intervalo de confianza al 95% obtenido tiene un 95% de probabilidades de contener el valor real del efecto”: Falso, recuerden que la propiedad de los intervalos de confianza no es esa. Piensen que el IC es un rango entre dos números, el efecto real o está o no está dentro de ese rango. Si estuviera dentro, su probabilidad sería 100% y si estuviera fuera, sería 0%. El 95% hace referencia a cuán seguido, otros intervalos de confianza al 95% de experimentos válidos contendrán el efecto real.
Hay otros dos errores comunes que me gustaría desarrollar. El primero tiene que ver con la parte previa a la ejecución del experimento, y el segundo tiene que ver a decisiones tomadas durante el experimento.
No realizar el cálculo de potencia
Si en general cuando realizan un test y este resulta no significativo, creen entonces que no hubo efecto, entonces es probable que estén siendo víctimas de este error.
Muchos experimentos se ejecutan sin haber calculado antes el tamaño muestral necesario. Esto en general produce 2 tipos de consecuencias importantes. El primero es no controlar por el riesgo de error tipo 1, el más conocido, el famoso alpha. El segundo es no controlar el riesgo del error tipo 2.
El riesgo de error tipo 2 es la probabilidad de no rechazar la hipótesis nula, cuando en verdad si existía un efecto, y suele presentarse con la sigla ß. La potencia de un experimento se da justamente con el cálculo 1 - ß.
¿Pero qué significa la potencia del experimento? Si nuestro ß es por ejemplo 0,1 o 10%, quiere decir que queremos controlar que en repetidos experimentos válidos, la probabilidad de no rechazar la hipótesis nula cuando en verdad si había efecto, sea solo el 10%. Entonces la potencia del experimento en este caso sería 100 - 10% = 90%. Diríamos que nuestro test se realizó a una potencia de 90%.
Y se preguntaran cómo está esto relacionado con el tamaño de los efectos. Resulta que un diseño experimental de este tipo bien hecho requiere que antes de que recolectemos los datos, es necesario haber establecido tanto una hipótesis nula, una hipótesis alternativa, el efecto mínimo que nos interesa poder observar, un alpha para controlar riesgo de error tipo 1, y un beta para controlar riesgo de error tipo 2. Al tener todos esos parámetros definidos, recién ahí podremos, a través de un test de potencia, calcular el tamaño muestral necesario, para que el experimento pueda controlar por todas esas definiciones.
¿Cuántos tests que realizaron hasta ahora, los diseñaron con un test de potencia previo? Todos aquellos que no tuvieron test de potencia previo, no controlaron entonces por el efecto mínimo a identificar, ni la potencia necesaria. Y por lo tanto muchos de ellos quizás no es que no tuvieron efecto, sino que no tuvieron el tamaño muestral suficiente para detectar un efecto como el observado con una determinada probabilidad. Realizaron un test sub potenciado.
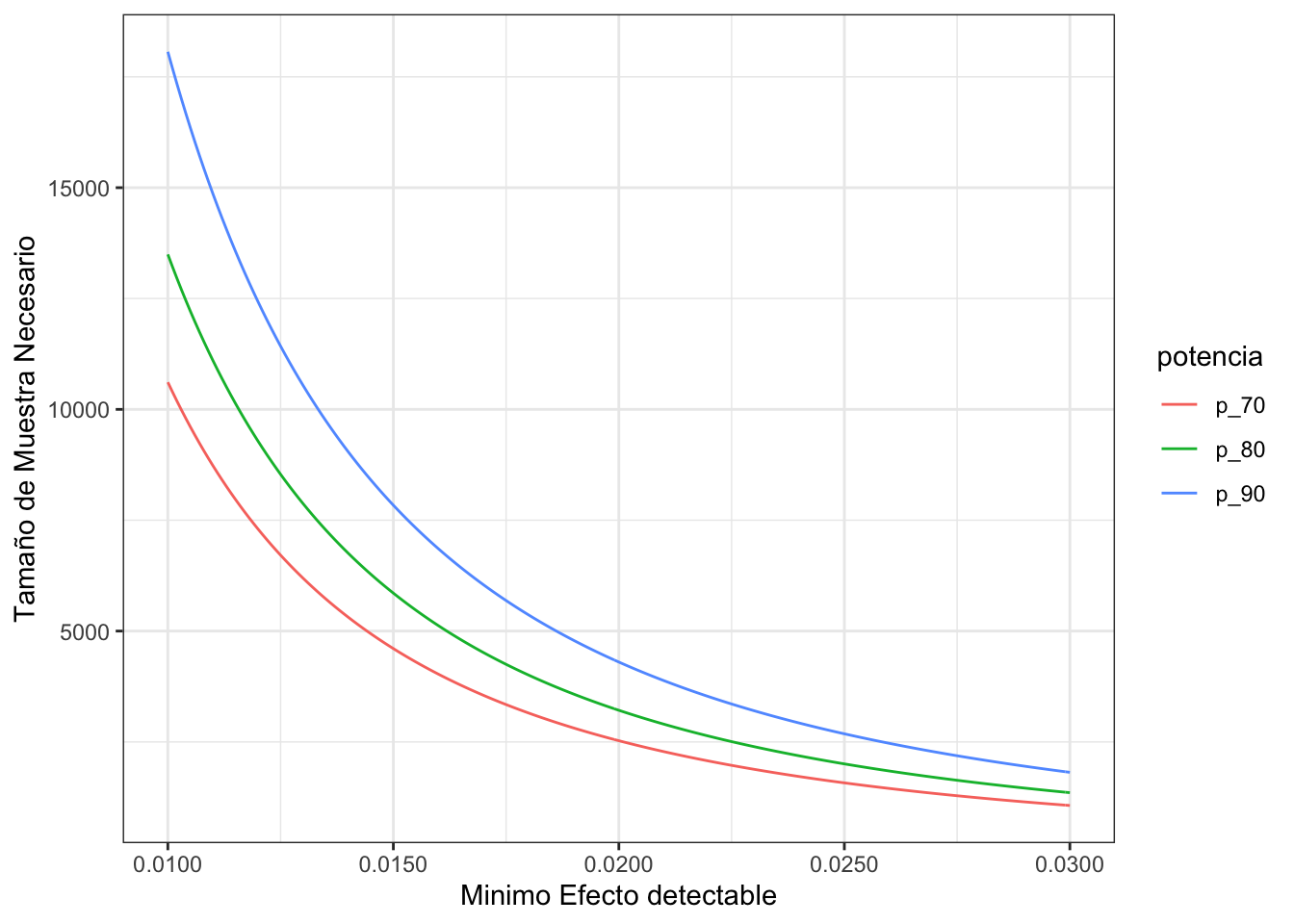
Como podrán ver en el gráfico anterior, con un determinado tamaño muestral y a una determinada potencia, hay un efecto mínimo detectable. Efectos menores a esos no serán detectados por el experimento con el fín de poder rechazar la hipótesis nula. Cuando se busca disminuir el riesgo de error tipo 2, osea aumentar la potencia, verán que el tamaño muestral necesario aumenta. O a una potencia fija, el tamaño muestral necesario aumenta a medida que me interesa detectar efectos más chicos.
Frenar el experimento antes o no frenarlo hasta obtener significancia.
Me he encontrado con muchos equipos que realizan ambas versiones de este error. Por lo general los motivos por el que lo cometen suelen estar ligados a una mala cultura de experimentación, donde el incentivo está simplemente en realizar la mayor cantidad de experimentos, sin velar por la calidad de los mismos. También es frecuente encontrarlo cuando el incentivo está en obtener significancia, solamente para poder justificar el experimento en sí mismo. Este problema por lo tanto tiene dos aristas, una relacionada a un bajo nivel de conocimiento estadístico, y otro a una errónea gestión de los objetivos de la experimentación en el equipo.
Empezaré por aclarar el error de no frenar un experimento hasta obtener significancia.
Recuerden lo que vimos en el error anterior, respecto al test de potencia. Un correcto diseño de experimento de este tipo, requiere definir ciertos parámetros, y eso nos devuelve el tamaño muestral necesario. Ese tamaño muestral entonces, es el que define cuando un experimento debe frenarse para controlar por los parámetros que decidimos.
Dejarlo correr más tiempo, con el fin de frenarlo sólo cuando se obtenga una significancia, no sólo es costoso para el negocio dado que durante todo ese tiempo se le está brindando una experiencia subóptima, sea control o variante, a una fracción de los usuarios, sino que además, está garantizado que vaya a obtener significancia.
¿Por qué? Porque los p-values no son fijos, van cambiando a medida que se obtienen las observaciones, y por lo tanto, la probabilidad de que un p-value sea del valor que nos interesa, en un tiempo infinito, es 1. Si yo dejo correr un experimento por tiempo indefinido, es seguro que en algún momento llegara al p-value que me interesa, pero eso no genera ningún tipo de validez sobre el procedimiento experimental que diseñamos.
Bajo esa misma línea nos encontramos con el típico caso de frenar los experimentos antes, sea por significancia o no. Fijense que recien les comenté que los p-values varían en el tiempo. Por lo tanto es esperable también que en un experimento cualquiera, una variante sea significativa (p-value menor al alpha que decidimos) en algún momento previo a las observaciones totales necesarias.
Eso no quiere decir que debemos frenar el experimento! De hecho, cuantas más veces miramos los datos recolectados por el experimento con intención de frenarlo, más probable es que nuestro experimento resulte en un Error de Tipo 1 (falso positivo).
Supongamos un experimento que luego del test de potencia, requiere 10000 observaciones, con un riesgo de falso positivo del 5%. Pero en este caso, sabemos de verdad que no hay efecto, dado que las dos variantes son idénticas. Ahora bien, decidimos mirar el experimento cada vez que se obtienen 100 observaciones, por un total de 100 miradas. Si al empezar el experimento teníamos solo un 5% de probabilidad de que resulte en un falso positivo, ahora cada vez que lo miramos tenemos un 5% de probabilidad de observar un falso positivo, por lo tanto cuanto más miremos, más aumentamos nuestro riesgo de cometer un error de tipo 1. Generalmente mirar solo 2 veces duplica el riesgo seleccionado. Mirar 5 veces multiplica el riesgo por 3, y mirar ya 10 veces lo cuadriplica. El cálculo de este efecto se puede verificar por simulaciones como en el trabajo de Armitage et. al. “Repeated Significance Tests on Accumulating Data”.
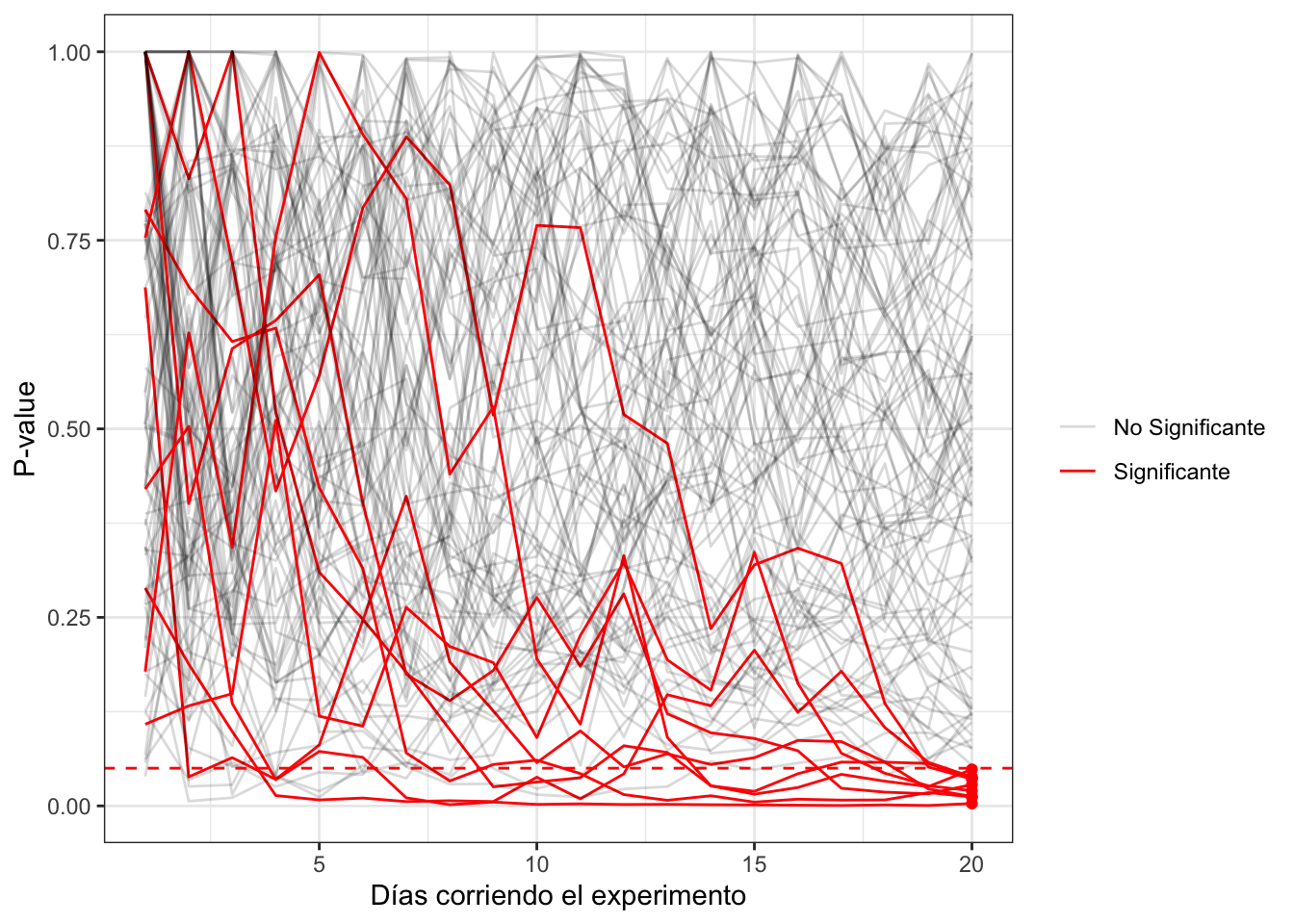
En el anterior gráfico podemos observar la evolución del p-value de muchas simulaciones de experimentos donde no había efecto. Si nos fijamos el p-value final, vemos como solo el 5% resultó significativo, que es el 5% de riesgo error tipo 1 que determinamos.
Pero miren que pasa en el siguiente gráfico, donde frenamos cada experimento cuando alcanzó significancia en algún momento de la recolección.
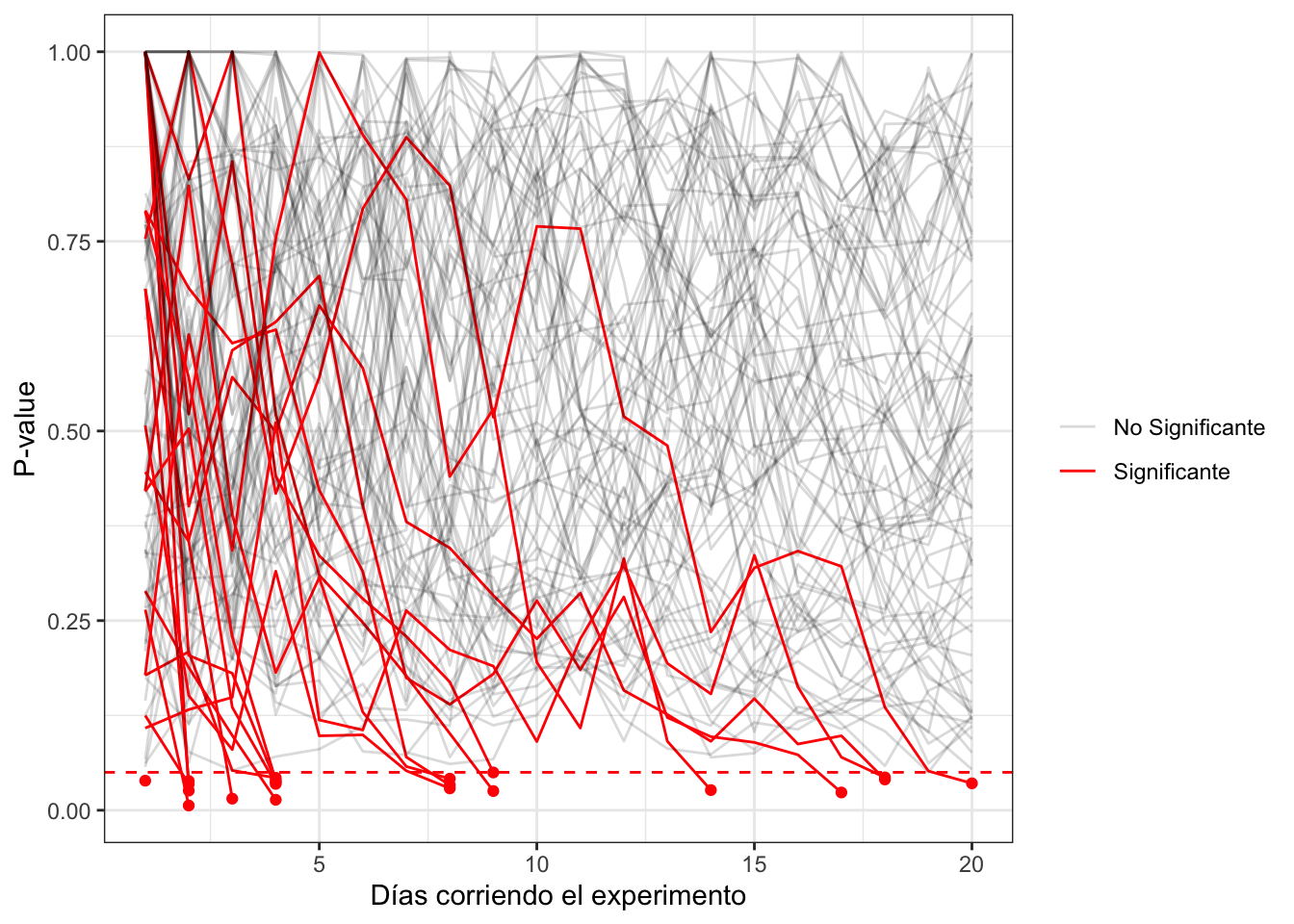
Como podrán ver, muchos más experimentos ahora son significantes. De hecho, el 22,68% de los experimentos simulados nos dan significantes, cuando en verdad ninguno tenía efecto!
Es por eso que en este tipo de tests, la decisión de cuándo se debe frenar el experimento es obtenida por el test de potencia y el tamaño muestral que nos devuelve dado los parámetros seleccionados.
Conclusiones
En el transcurso de este post vimos los 4 errores respecto a A/B tests más frecuentes en mi experiencia. Habran notado que los mismos pueden darse tanto antes de empezar el experimento, como durante y hasta después de haberlo terminado. Experimentar es dificil, y es lógico que lo sea dado que se está tratando de inferir una verdad de comportamiento respecto a una población que no podemos observar en su totalidad. Pero eso no quiere decir que no se debería experimentar. Por eso creo que es importante saber dónde es que podemos equivocarnos, para mitigar la posibilidad de perder tiempo y esfuerzo en experimentos no válidos. Espero que esta nota haya ayudado a lograr ese objetivo.
Gracias por leer mi blog!
Si te gustó lo que leiste te invito a que te sumes al newsletter para recibir un mail semanal con el nuevo contenido y novedades. O podes apoyarme con su desarrollo invitandome un cafe :) Muchas gracias!


Share this post
Twitter
Facebook
Reddit
LinkedIn
Email